Materi matematika eksponen dan logaritma merupakan bagian penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang, mulai dari keuangan hingga ilmu pengetahuan. Konsep eksponen dan logaritma memungkinkan kita untuk memahami dan menganalisis pertumbuhan dan peluruhan, serta menyelesaikan berbagai persamaan dan pertidaksamaan.
Materi ini akan membahas definisi, aturan, jenis-jenis, penerapan dalam persamaan dan pertidaksamaan, serta aplikasi dalam berbagai konteks. Dari konsep dasar hingga contoh soal, materi ini akan memandu Anda dalam memahami dan menguasai materi eksponen dan logaritma.
Definisi dan Konsep Dasar
Eksponen dan logaritma merupakan dua konsep penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang. Kedua konsep ini saling berkaitan erat dan sering digunakan untuk menyelesaikan masalah yang melibatkan pertumbuhan atau penurunan eksponensial.
Pengertian Eksponen dan Logaritma
Eksponen adalah operasi matematika yang menunjukkan perkalian berulang dari suatu bilangan. Logaritma adalah operasi invers dari eksponen, yang digunakan untuk mencari eksponen yang sesuai dengan suatu bilangan. Secara sederhana, eksponen menunjukkan berapa kali suatu bilangan dikalikan dengan dirinya sendiri, sedangkan logaritma menunjukkan berapa kali suatu bilangan pokok harus dikalikan dengan dirinya sendiri untuk mendapatkan suatu bilangan tertentu.
Contoh Penerapan dalam Kehidupan Sehari-hari
Eksponen dan logaritma diterapkan dalam berbagai aspek kehidupan sehari-hari, seperti perhitungan bunga majemuk, pertumbuhan populasi, dan pengukuran intensitas suara. Misalnya, perhitungan bunga majemuk pada deposito bank melibatkan konsep eksponen. Pertumbuhan populasi bakteri juga dapat dimodelkan dengan fungsi eksponen. Pengukuran intensitas suara menggunakan logaritma untuk mengukur skala desibel.
Perbedaan Fungsi Eksponen dan Logaritma
Fungsi eksponen dan logaritma memiliki perbedaan mendasar dalam bentuk dan sifat-sifatnya. Fungsi eksponen menggambarkan pertumbuhan atau penurunan yang cepat, sedangkan fungsi logaritma menggambarkan pertumbuhan yang lambat dan cenderung mendekati asimtot. Tabel berikut membandingkan sifat-sifat fungsi eksponen dan logaritma.
| Sifat | Fungsi Eksponen | Fungsi Logaritma |
|---|---|---|
| Bentuk Umum | f(x) = ax | f(x) = loga(x) |
| Domain | Semua bilangan real (x ∈ ℝ) | x > 0 (x ∈ ℝ+) |
| Range | Semua bilangan real positif (f(x) ∈ ℝ+) | Semua bilangan real (f(x) ∈ ℝ) |
| Asimtot | Sumbu x (x = 0) | Sumbu y (y = 0) |
| Grafik | Meningkat secara eksponensial | Meningkat secara monoton |
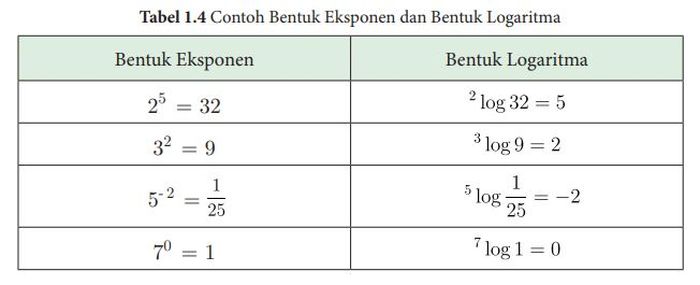
Mengubah Bentuk Eksponen ke Logaritma dan Sebaliknya
Misalnya, persamaan eksponen 23 = 8 dapat diubah menjadi bentuk logaritma sebagai log 2(8) = 3. Sebaliknya, persamaan logaritma log 5(25) = 2 dapat diubah menjadi bentuk eksponen sebagai 5 2 = 25.
Aturan-aturan Eksponen dan Logaritma

Setelah memahami definisi dan konsep dasar eksponen dan logaritma, kita akan menjelajahi aturan-aturan yang memudahkan dalam melakukan operasi pada keduanya. Pemahaman aturan ini sangat penting untuk memecahkan berbagai permasalahan matematika.
Aturan-aturan Operasi Eksponen
Operasi eksponen melibatkan perkalian berulang suatu bilangan. Beberapa aturan dasar dalam operasi eksponen meliputi perkalian, pembagian, dan perpangkatan.
- Perkalian Eksponen dengan Basis yang Sama: Untuk mengalikan eksponen dengan basis yang sama, pangkatkan basis dengan jumlah eksponen.
- Pembagian Eksponen dengan Basis yang Sama: Untuk membagi eksponen dengan basis yang sama, pangkatkan basis dengan selisih eksponen.
- Pangkat dari Pangkat: Untuk menaikkan suatu eksponen ke pangkat lain, kalikan eksponen-eksponen tersebut.
- Eksponen Nol: Setiap bilangan yang dipangkatkan nol sama dengan satu (kecuali nol dipangkatkan nol).
- Eksponen Negatif: Eksponen negatif menunjukkan kebalikan dari pangkat positif. Jika terdapat eksponen negatif, dapat dituliskan sebagai pecahan dengan pangkat positif.
| Aturan | Rumus | Contoh |
|---|---|---|
| Perkalian Eksponen | am × an = am+n | 23 × 22 = 25 = 32 |
| Pembagian Eksponen | am ÷ an = am-n | 25 ÷ 22 = 23 = 8 |
| Pangkat dari Pangkat | (am)n = amn | (23)2 = 26 = 64 |
| Eksponen Nol | a0 = 1 (a ≠ 0) | 50 = 1 |
| Eksponen Negatif | a-n = 1/an | 2-3 = 1/23 = 1/8 |
Aturan-aturan Operasi Logaritma
Logaritma adalah invers dari eksponen. Aturan-aturan logaritma mencerminkan aturan eksponen. Beberapa aturan penting meliputi logaritma perkalian, pembagian, dan perpangkatan.
- Logaritma Perkalian: Logaritma dari perkalian dua bilangan sama dengan jumlah logaritma dari masing-masing bilangan.
- Logaritma Pembagian: Logaritma dari pembagian dua bilangan sama dengan selisih logaritma dari masing-masing bilangan.
- Logaritma Pangkat: Logaritma dari suatu bilangan yang dipangkatkan sama dengan pangkat dikalikan dengan logaritma bilangan tersebut.
- Perubahan Basis Logaritma: Memungkinkan perhitungan logaritma dengan basis yang berbeda.
| Aturan | Rumus | Contoh (basis 10) |
|---|---|---|
| Logaritma Perkalian | log(ab) = log(a) + log(b) | log(10×100) = log(10) + log(100) = 1 + 2 = 3 |
| Logaritma Pembagian | log(a/b) = log(a)
|
log(100/10) = log(100)
|
| Logaritma Pangkat | log(ab) = b log(a) | log(103) = 3 log(10) = 3 × 1 = 3 |
Hubungan Antara Aturan Eksponen dan Logaritma
Aturan-aturan eksponen dan logaritma saling berkaitan erat. Hubungan ini dapat dilihat pada contoh-contoh di atas. Aturan-aturan logaritma merupakan invers dari aturan-aturan eksponen. Memahami hubungan ini sangat membantu dalam menyelesaikan berbagai soal matematika yang melibatkan eksponen dan logaritma.
Jenis-jenis Fungsi Eksponen dan Logaritma: Materi Matematika Eksponen Dan Logaritma

Pemahaman tentang berbagai jenis fungsi eksponen dan logaritma sangat penting dalam berbagai aplikasi matematika dan ilmu pengetahuan. Fungsi-fungsi ini memiliki karakteristik unik yang memengaruhi bentuk grafik dan penerapannya.
Jenis-jenis Fungsi Eksponen
Beberapa jenis fungsi eksponen yang umum digunakan meliputi:
- Fungsi Eksponen Dasar: Bentuk paling sederhana, seperti f(x) = a x, di mana ‘a’ adalah basis (bilangan real positif yang bukan 1).
- Fungsi Eksponen Bergeser: Fungsi eksponen yang mengalami pergeseran vertikal atau horizontal. Misalnya, f(x) = a x + b (pergeseran vertikal) atau f(x) = a x-c (pergeseran horizontal).
- Fungsi Eksponen Dikalikan: Fungsi eksponen yang dikalikan dengan konstanta. Misalnya, f(x) = k
– a x, di mana ‘k’ adalah konstanta.
Contoh Grafik Fungsi Eksponen dan Logaritma
Grafik fungsi eksponen umumnya berbentuk kurva yang meningkat atau menurun secara eksponensial, bergantung pada nilai basis. Grafik fungsi logaritma merupakan invers dari fungsi eksponen. Contoh grafik dapat bervariasi tergantung pada basis dan nilai konstanta.
Sebagai ilustrasi, grafik f(x) = 2 x akan meningkat secara eksponensial dari kiri ke kanan, sedangkan grafik f(x) = (1/2) x akan menurun secara eksponensial. Grafik f(x) = log 2(x) akan meningkat secara logaritmik.
Pengaruh Nilai Basis terhadap Grafik Fungsi Eksponen
Nilai basis ‘a’ pada fungsi eksponen f(x) = a x sangat memengaruhi bentuk grafik. Jika 0 < a < 1, grafik akan menurun secara eksponensial. Jika a > 1, grafik akan meningkat secara eksponensial. Semakin besar nilai ‘a’, semakin cepat grafik meningkat.
Menentukan Domain dan Range Fungsi Eksponen dan Logaritma
Domain suatu fungsi adalah himpunan semua nilai input yang dapat diterima, sedangkan range adalah himpunan semua nilai output yang mungkin. Secara umum, domain fungsi eksponen f(x) = a x adalah semua bilangan real (x ∈ ℝ). Range fungsi eksponen adalah semua bilangan real positif (y ∈ (0, ∞)). Untuk fungsi logaritma, domainnya adalah bilangan real positif, dan range-nya adalah semua bilangan real.
Perbedaan Sifat Fungsi Eksponen dan Logaritma dengan Basis Berbeda
Perbedaan utama terletak pada bagaimana basis memengaruhi pertumbuhan atau penurunan fungsi. Fungsi eksponen dengan basis yang lebih besar dari 1 akan meningkat lebih cepat dibandingkan dengan fungsi eksponen dengan basis yang lebih kecil dari 1. Fungsi logaritma dengan basis yang lebih besar dari 1 akan memiliki grafik yang naik lebih cepat dibandingkan dengan fungsi logaritma dengan basis yang lebih kecil dari 1.
Perbedaan ini penting dalam aplikasi, seperti dalam pertumbuhan populasi atau pengukuran intensitas suatu peristiwa.
Penerapan dalam Persamaan dan Pertidaksamaan
Penerapan eksponen dan logaritma dalam persamaan dan pertidaksamaan sangat penting dalam berbagai bidang, seperti ilmu pengetahuan, teknik, dan ekonomi. Memahami cara menyelesaikan persamaan dan pertidaksamaan eksponen dan logaritma akan memperluas pemahaman Anda tentang konsep-konsep ini.
Contoh Persamaan Eksponen Sederhana
Persamaan eksponen melibatkan variabel dalam eksponen. Berikut beberapa contoh persamaan eksponen sederhana:
- 2 x = 8
- 5 x+1 = 125
- e 2x = 10
Penyelesaian Persamaan Eksponen
Untuk menyelesaikan persamaan eksponen, seringkali kita perlu mengubah basisnya agar sama. Contohnya, jika basisnya sama, maka eksponennya juga harus sama. Jika basisnya berbeda, kita bisa menggunakan logaritma untuk menyelesaikannya.
- Contoh 1: 2 x = 8. Karena 8 = 2 3, maka persamaan menjadi 2 x = 2 3. Dengan demikian, x = 3.
- Contoh 2: 5 x+1 = 125. Karena 125 = 5 3, maka persamaan menjadi 5 x+1 = 5 3. Dengan demikian, x+1 = 3, dan x = 2.
- Contoh 3: e 2x = 10. Dengan menerapkan logaritma natural pada kedua ruas, kita dapatkan 2x = ln(10). Sehingga x = ln(10)/2.
Contoh Pertidaksamaan Eksponen Sederhana
Pertidaksamaan eksponen melibatkan perbandingan nilai eksponen. Berikut beberapa contoh:
- 2 x > 16
- 3 x ≤ 1/9
Penyelesaian Pertidaksamaan Eksponen
Untuk menyelesaikan pertidaksamaan eksponen, langkah-langkahnya mirip dengan persamaan eksponen, namun perlu diperhatikan tanda pertidaksamaan. Penting untuk memperhatikan apakah basis lebih besar dari 1 atau antara 0 dan 1. Hal ini berpengaruh pada arah tanda pertidaksamaan.
- Contoh 1: 2 x > 16. Karena 16 = 2 4, maka pertidaksamaan menjadi 2 x > 2 4. Karena basis 2 lebih besar dari 1, maka x > 4.
- Contoh 2: 3 x ≤ 1/9. Karena 1/9 = 3 -2, maka pertidaksamaan menjadi 3 x ≤ 3 -2. Karena basis 3 lebih besar dari 1, maka x ≤ -2.
Penerapan dalam Dunia Nyata
Eksponen dan logaritma memiliki aplikasi yang luas dalam kehidupan sehari-hari. Berikut beberapa contoh:
- Pertumbuhan Penduduk: Pertumbuhan penduduk sering dimodelkan dengan persamaan eksponen. Contohnya, jika populasi suatu kota tumbuh sebesar 5% per tahun, maka persamaan eksponen dapat digunakan untuk memprediksi populasi di masa depan.
- Peluruhan Radioaktif: Peluruhan radioaktif dapat dimodelkan dengan persamaan eksponen. Contohnya, waktu paruh suatu unsur radioaktif dapat dihitung menggunakan persamaan eksponen. Ini penting dalam bidang medis dan arkeologi.
Aplikasi dan Contoh Soal
Materi eksponen dan logaritma memiliki beragam aplikasi dalam berbagai bidang, mulai dari keuangan hingga sains. Pemahaman yang baik akan membantu menyelesaikan permasalahan nyata dengan efektif.
Contoh Soal Keuangan
Pertumbuhan investasi seringkali dihitung menggunakan rumus eksponen. Misalnya, investasi sebesar Rp 10.000.000 dengan suku bunga 5% per tahun selama 10 tahun. Berapa besar investasi tersebut?
A = P(1 + r)t
dimana:
A = jumlah investasi setelah t tahun
P = jumlah investasi awal
r = suku bunga per tahun
t = waktu dalam tahun
Dengan P = 10.000.000, r = 0.05, dan t = 10, maka:
A = 10.000.000(1 + 0.05) 10 = 10.000.000(1.05) 10 ≈ 16.288.946,26
Jadi, investasi tersebut akan bernilai sekitar Rp 16.288.946,26 setelah 10 tahun.
Contoh Soal Pertumbuhan Populasi
Pertumbuhan populasi bakteri dapat dimodelkan dengan persamaan eksponen. Misalnya, populasi bakteri awal 1000 dan berlipat ganda setiap 2 jam. Berapa banyak bakteri setelah 10 jam?
N(t) = N0
2t/2
dimana:
N(t) = jumlah bakteri pada waktu t
N 0 = jumlah bakteri awal
t = waktu dalam jam
Dengan N 0 = 1000 dan t = 10, maka:
N(10) = 1000
– 2 10/2 = 1000
– 2 5 = 1000
– 32 = 32.000
Setelah 10 jam, terdapat 32.000 bakteri.
Aplikasi Logaritma dalam Fisika
Skala Richter digunakan untuk mengukur kekuatan gempa bumi. Besarnya gempa diukur menggunakan logaritma. Misalnya, gempa dengan magnitudo 6 pada skala Richter memiliki intensitas 10 6 kali lebih besar dari gempa dengan magnitudo 0. Bagaimana cara menghitung selisih intensitas antara gempa 7 dan 5 pada skala Richter?
Perbedaan intensitas antara gempa 7 dan 5 adalah 10 7 / 10 5 = 10 2 = 100. Gempa dengan magnitudo 7 memiliki intensitas 100 kali lebih besar dari gempa dengan magnitudo 5.
Penerapan dalam Persamaan Trigonometri
Logaritma dapat digunakan untuk menyelesaikan persamaan trigonometri yang melibatkan eksponen. Misalnya, tentukan nilai x yang memenuhi sin(x) = 0.5. Solusi tersebut dapat ditemukan menggunakan logaritma.
Dalam kasus ini, kita tidak dapat langsung menemukan nilai x tanpa bantuan kalkulator atau tabel trigonometri. Persamaan ini membutuhkan fungsi invers trigonometri, seperti arcsin.
Ilustrasi Konsep
Pemahaman konsep eksponen dan logaritma akan lebih mudah dengan ilustrasi visual. Grafik fungsi dan diagram dapat membantu kita membayangkan bagaimana konsep ini bekerja dalam berbagai situasi, seperti pertumbuhan dan skala besar.
Grafik Fungsi Eksponen dan Logaritma
Grafik fungsi eksponen dan logaritma memperlihatkan bagaimana nilai fungsi berubah seiring perubahan variabel. Perhatikan bahwa bentuk grafik akan berbeda tergantung pada basis fungsi.
- Grafik fungsi eksponen dengan basis b > 1 akan selalu naik, sedangkan grafik dengan 0 < b < 1 akan selalu turun. Semakin besar nilai b, semakin cepat pertumbuhan eksponen.
- Grafik fungsi logaritma selalu melalui titik (1,0) dan bentuknya merupakan cerminan dari grafik fungsi eksponen.
- Contoh: Grafik fungsi f(x) = 2x akan menunjukkan pertumbuhan eksponen yang lebih cepat dibandingkan dengan grafik f(x) = 1.5x.
Ilustrasi Pertumbuhan Eksponen
Pertumbuhan eksponen menggambarkan peningkatan nilai secara cepat. Bayangkan populasi bakteri yang berlipat ganda setiap jam. Ilustrasi ini bisa ditunjukkan dengan grafik yang menunjukkan peningkatan eksponensial jumlah bakteri terhadap waktu.
Contoh: Ilustrasi grafik dapat memperlihatkan bagaimana populasi bakteri tumbuh secara eksponensial. Grafik akan memperlihatkan peningkatan yang cepat dalam jumlah bakteri seiring waktu. Semakin cepat pertumbuhan, semakin curam grafik.
Ilustrasi Pengukuran Skala Besar, Materi matematika eksponen dan logaritma
Logaritma berguna untuk mengukur skala besar, seperti magnitudo gempa bumi atau intensitas bunyi. Dengan logaritma, kita dapat merangkum data yang memiliki rentang nilai yang sangat besar dalam skala yang lebih mudah dipahami.
- Sebagai contoh, skala Richter digunakan untuk mengukur magnitudo gempa bumi. Setiap kenaikan satu satuan pada skala Richter menunjukkan peningkatan intensitas gempa bumi sebesar 10 kali lipat.
- Ilustrasi dapat berupa grafik yang menunjukkan hubungan antara magnitudo gempa bumi (skala logaritmik) dan energi yang dilepaskan.
Perbandingan Pertumbuhan Eksponen dan Linear
Grafik dapat digunakan untuk membandingkan pertumbuhan eksponen dan linear. Pertumbuhan linear menunjukkan peningkatan konstan, sedangkan pertumbuhan eksponen menunjukkan peningkatan yang semakin cepat.
| Jenis Pertumbuhan | Deskripsi | Ilustrasi Grafik |
|---|---|---|
| Linear | Peningkatan konstan seiring waktu. | Garis lurus. |
| Eksponen | Peningkatan yang semakin cepat seiring waktu. | Kurva yang naik secara cepat. |
Contoh: Grafik yang menunjukkan pertumbuhan penduduk suatu kota dengan pertumbuhan linear akan berupa garis lurus. Sementara itu, grafik yang menunjukkan pertumbuhan jumlah virus dalam suatu eksperimen akan berupa kurva yang menunjukkan pertumbuhan eksponensial yang semakin cepat.
Ringkasan Akhir
Semoga materi ini memberikan pemahaman yang komprehensif tentang eksponen dan logaritma. Dengan menguasai konsep dan aturannya, Anda dapat menyelesaikan berbagai permasalahan matematika dan mengaplikasikannya dalam berbagai bidang ilmu. Selamat belajar!