Materi matematika garis singgung lingkaran akan membahas secara detail tentang hubungan antara garis dan lingkaran. Kita akan mempelajari definisi, sifat-sifat, persamaan, dan aplikasi garis singgung dalam berbagai konteks geometri.
Dari pengertian dasar hingga contoh soal dan latihan, materi ini dirancang untuk memberikan pemahaman yang komprehensif. Kita akan menjelajahi bagaimana garis singgung berhubungan dengan jari-jari, dan bagaimana mencari persamaan garis singgung dari berbagai posisi terhadap lingkaran.
Definisi dan Konsep Dasar

Garis singgung lingkaran adalah garis yang hanya menyinggung lingkaran tepat di satu titik. Konsep ini sangat penting dalam geometri dan memiliki aplikasi luas dalam berbagai bidang, seperti teknik dan desain.
Pengertian Garis Singgung
Garis singgung lingkaran didefinisikan sebagai garis yang tepat menyentuh lingkaran di satu titik dan tegak lurus dengan jari-jari lingkaran pada titik singgung tersebut. Titik singgung ini merupakan satu-satunya titik persekutuan antara garis dan lingkaran.
Ilustrasi Visual
Bayangkan sebuah lingkaran. Garis singgung dapat berada di berbagai posisi. Ada garis singgung yang berada di atas lingkaran, di bawah lingkaran, di kiri, atau di kanan lingkaran. Semua garis singgung tersebut hanya menyentuh lingkaran di satu titik dan tegak lurus dengan jari-jari di titik singgung. Bayangkan pula lingkaran yang berbeda ukuran, posisi garis singgung tetap memiliki sifat yang sama.
Sebuah garis singgung tidak akan pernah memotong lingkaran pada dua titik atau lebih.
Sifat-Sifat Garis Singgung
Berikut beberapa sifat penting garis singgung:
- Garis singgung tegak lurus dengan jari-jari lingkaran pada titik singgung.
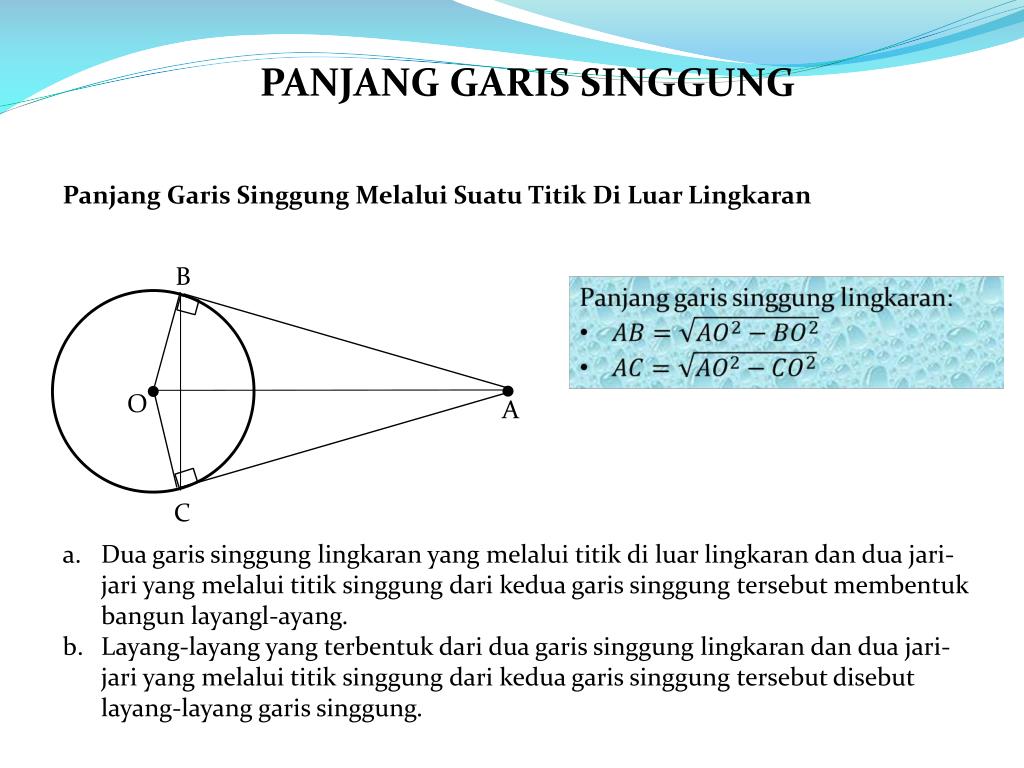
- Dari satu titik di luar lingkaran, hanya dapat ditarik dua garis singgung yang berbeda.
- Panjang kedua garis singgung dari titik luar lingkaran ke titik singgung pada lingkaran sama panjang.
Perbedaan Garis Singgung dan Garis Lain yang Memotong Lingkaran
| Aspek | Garis Singgung | Garis yang Memotong Lingkaran |
|---|---|---|
| Jumlah Titik Persekutuan | Satu titik | Dua titik |
| Kedudukan terhadap Jari-jari | Tegak lurus dengan jari-jari pada titik singgung | Membentuk sudut dengan jari-jari |
| Sifat Panjang Garis Singgung | Dari satu titik di luar lingkaran, panjang kedua garis singgung sama. | Panjang garis tidak sama. |
Persamaan Garis Singgung: Materi Matematika Garis Singgung Lingkaran
Memahami persamaan garis singgung pada lingkaran sangat penting dalam geometri analitik. Dengan rumus yang tepat, kita dapat menentukan persamaan garis yang menyentuh lingkaran pada satu titik tertentu.
Rumus Umum Persamaan Garis Singgung
Persamaan umum garis singgung pada lingkaran dengan pusat (a, b) dan jari-jari r adalah:
y – y1 = m(x – x 1)
dimana:
- m adalah gradien garis singgung, yang dapat dihitung dengan turunan.
- (x 1, y 1) adalah koordinat titik singgung pada lingkaran.
Menentukan Persamaan Garis Singgung pada Titik Tertentu
Langkah-langkah untuk menentukan persamaan garis singgung pada titik tertentu pada lingkaran:
- Identifikasi Koordinat Titik Singgung: Tentukan koordinat titik (x 1, y 1) pada lingkaran yang akan menjadi titik singgung.
- Menentukan Gradien (m): Hitung gradien garis singgung dengan mencari turunan pertama persamaan lingkaran terhadap x pada titik (x 1, y 1). Jika persamaan lingkaran dalam bentuk x 2 + y 2 = r 2, turunannya dapat digunakan untuk menentukan kemiringan garis singgung.
- Substitusi: Substitusikan nilai x 1, y 1, dan m yang telah ditemukan ke dalam persamaan umum garis singgung.
- Sederhanakan: Sederhanakan persamaan garis singgung untuk mendapatkan bentuk yang lebih rapi.
Contoh Soal dan Penyelesaian
Misalkan kita ingin mencari persamaan garis singgung pada titik (1, √3) pada lingkaran x 2 + y 2 = 4.
- Titik Singgung: (x 1, y 1) = (1, √3).
- Gradien (m): Turunan pertama dari x 2 + y 2 = 4 adalah 2x + 2y(dy/dx) = 0. Dari sini, dy/dx = -x/y. Pada titik (1, √3), m = -1/√3.
- Substitusi: y – √3 = (-1/√3)(x – 1).
- Sederhanakan: y – √3 = (-1/√3)x + 1/√3. Persamaan garis singgung adalah y = (-1/√3)x + (1 + √3)/√3.
Contoh Persamaan Lingkaran dan Garis Singgungnya
| Persamaan Lingkaran | Persamaan Garis Singgung |
|---|---|
| x2 + y2 = 25 | y = -4/3 x + 25/3 |
| (x – 2)2 + (y + 1)2 = 9 | y = 3x – 10 |
| x2 + y2 = 16 | y = 3/4 x + √7 |
Garis Singgung dan Jari-jari
Dalam geometri, garis singgung lingkaran memiliki hubungan khusus dengan jari-jari lingkaran. Hubungan ini sangat penting dalam berbagai aplikasi matematika dan ilmu terapan.
Hubungan Tegak Lurus Garis Singgung dan Jari-jari, Materi matematika garis singgung lingkaran
Garis singgung pada suatu titik pada lingkaran selalu tegak lurus terhadap jari-jari yang menghubungkan titik pusat lingkaran dengan titik singgung tersebut. Teorema ini merupakan prinsip fundamental dalam geometri analitik dan trigonometri.
Ilustrasi Visual
Bayangkan sebuah lingkaran dengan titik pusat O. Pada lingkaran tersebut, terdapat titik singgung T. Jari-jari yang menghubungkan titik pusat O dengan titik singgung T akan membentuk sudut 90 derajat dengan garis singgung yang melalui titik T. Gambar ini menggambarkan bagaimana garis singgung tegak lurus terhadap jari-jari di titik singgung.
Menentukan Panjang Jari-jari
Jika diketahui persamaan garis singgung dan titik singgung, kita dapat menentukan panjang jari-jari lingkaran. Berikut langkah-langkahnya:
- Cari persamaan lingkaran yang memuat titik singgung. Perlu diingat bahwa jari-jari lingkaran adalah tegak lurus dengan garis singgung di titik singgung.
- Tentukan gradien garis singgung. Ingat bahwa gradien garis singgung dan jari-jari yang menghubungkan titik singgung dengan pusat lingkaran saling tegak lurus, sehingga perkalian gradien keduanya sama dengan -1.
- Tentukan persamaan jari-jari menggunakan gradien yang telah ditemukan dan titik singgung.
- Tentukan koordinat titik pusat lingkaran.
- Hitung jarak antara titik pusat lingkaran dan titik singgung. Jarak tersebut merupakan panjang jari-jari lingkaran.
Sebagai contoh, jika persamaan garis singgung adalah y = 2x + 3 dan titik singgung adalah (1, 5), maka kita dapat mencari persamaan jari-jari yang tegak lurus dengan garis singgung tersebut di titik (1, 5). Gradien garis singgung adalah 2, sehingga gradien jari-jari adalah -1/2. Dengan informasi ini dan titik singgung, kita dapat mencari persamaan jari-jari. Setelah mendapatkan persamaan jari-jari, kita bisa menentukan koordinat titik pusat lingkaran dan menghitung panjang jari-jari.
Garis Singgung dari Titik Luar Lingkaran
Menentukan persamaan garis singgung dari titik di luar lingkaran melibatkan beberapa langkah penting. Memahami konsep ini memungkinkan kita untuk menggambar dan menghitung garis-garis yang menyentuh lingkaran tepat pada satu titik.
Penentuan Persamaan Garis Singgung
Untuk mencari persamaan garis singgung dari suatu titik di luar lingkaran, kita perlu menggunakan rumus yang tepat. Prosesnya biasanya melibatkan beberapa langkah, dimulai dengan mencari titik-titik pada lingkaran yang dilalui garis singgung tersebut. Setelah titik-titik tersebut ditemukan, persamaan garis singgung dapat dihitung dengan menggunakan rumus yang sesuai.
Contoh Soal dan Penyelesaian
Berikut contoh soal dan penyelesaiannya untuk mencari persamaan garis singgung dari titik di luar lingkaran:
-
Soal: Tentukan persamaan garis singgung lingkaran x 2 + y 2 = 25 dari titik (7, 0).
-
Penyelesaian:
Langkah pertama adalah menentukan jarak dari titik (7, 0) ke pusat lingkaran (0, 0). Jaraknya adalah √(7 2 + 0 2) = 7. Jarak ini harus lebih besar dari jari-jari lingkaran (r = 5) untuk memastikan titik tersebut berada di luar lingkaran. Selanjutnya, kita cari gradien garis yang menghubungkan titik (7, 0) dan titik pada lingkaran. Setelah mendapatkan gradien, kita dapat menentukan persamaan garis singgung yang melalui titik tersebut.Titik pada lingkaran yang membentuk garis singgung dapat dicari dengan memanfaatkan sifat geometri dan persamaan lingkaran. Dua garis singgung dapat ditarik dari titik (7, 0) ke lingkaran. Dengan menggabungkan konsep geometri dan aljabar, persamaan garis singgung tersebut dapat ditentukan.
Sketsa Dua Garis Singgung
Berikut sketsa yang menunjukkan dua garis singgung dari satu titik di luar lingkaran:
Sketsa menunjukkan titik di luar lingkaran yang ditarik dua garis singgung. Kedua garis singgung tersebut akan menyentuh lingkaran tepat pada satu titik. Perhatikan bahwa kedua garis singgung ini akan membentuk sudut yang sama dengan jari-jari lingkaran di titik singgungnya.
Ilustrasi Visual
Bayangkan sebuah lingkaran dengan pusat di titik asal (0, 0). Dari sebuah titik di luar lingkaran, misalnya (7, 0), kita tarik dua garis lurus yang menyentuh lingkaran pada dua titik berbeda. Kedua garis tersebut membentuk sudut siku-siku dengan jari-jari lingkaran pada titik singgungnya. Ini adalah ilustrasi visual dari dua garis singgung yang ditarik dari titik di luar lingkaran.
Aplikasi dalam Masalah Geometri

Penerapan konsep garis singgung lingkaran pada masalah geometri sangatlah penting. Pemahaman tentang garis singgung dapat membantu menyelesaikan berbagai permasalahan, mulai dari menentukan panjang garis singgung hingga menghitung luas bangun datar yang melibatkan lingkaran.
Penerapan dalam Perhitungan Panjang Garis Singgung
Konsep garis singgung lingkaran memungkinkan perhitungan panjang garis singgung dari titik di luar lingkaran. Perhitungan ini memanfaatkan teorema Pythagoras. Misalnya, jika diketahui jarak titik ke pusat lingkaran dan jari-jari lingkaran, maka panjang garis singgung dapat dihitung. Perhitungan ini sering digunakan dalam masalah geometri yang melibatkan posisi titik dan lingkaran.
Contoh:
Sebuah titik berada 10 cm dari pusat lingkaran dengan jari-jari 6 cm. Hitunglah panjang garis singgung dari titik tersebut ke lingkaran. Berdasarkan teorema Pythagoras, panjang garis singgung ( s) dapat dihitung dengan rumus s2 = d2
– r2, di mana d adalah jarak titik ke pusat lingkaran dan r adalah jari-jari lingkaran. Dengan demikian, s2 = 10 2
-6 2 = 100 – 36 = 64.
Maka, s = √64 = 8 cm. Jadi, panjang garis singgungnya adalah 8 cm.
Penerapan dalam Perhitungan Luas Bangun Datar
Konsep garis singgung dapat digunakan untuk menghitung luas bangun datar yang melibatkan lingkaran. Misalnya, dalam kasus segitiga yang dibatasi oleh garis singgung dan busur lingkaran, luas segitiga dapat dihitung dengan menggunakan panjang garis singgung dan jari-jari lingkaran.
Contoh:
Bayangkan segitiga yang dibatasi oleh dua garis singgung dan busur lingkaran. Misalkan panjang kedua garis singgungnya sama, masing-masing 12 cm, dan jari-jari lingkaran adalah 5 cm. Untuk menghitung luas segitiga tersebut, kita perlu menentukan tinggi segitiga tersebut. Garis yang menghubungkan titik singgung ke pusat lingkaran tegak lurus dengan garis singgung. Dengan teorema Pythagoras, jarak titik singgung ke pusat lingkaran adalah 13 cm.
Kemudian, luas segitiga dapat dihitung dengan rumus Luas = 1/2 x alas x tinggi. Dalam kasus ini, tinggi segitiga adalah jarak dari pusat lingkaran ke garis singgung, yang merupakan jari-jari lingkaran. Luas segitiga = 1/2 x (12 cm) x (5 cm) = 30 cm 2.
Penentuan Luas Daerah yang Dibatasi oleh Garis Singgung dan Busur Lingkaran
Dalam geometri, terdapat situasi di mana kita perlu menentukan luas daerah yang dibatasi oleh garis singgung dan busur lingkaran. Metode perhitungannya bergantung pada bentuk geometri yang terbentuk. Seringkali melibatkan perhitungan luas segitiga dan sektor lingkaran.
Contoh:
Bayangkan sebuah daerah yang dibatasi oleh dua garis singgung dan busur lingkaran. Garis singgung membentuk segitiga di luar lingkaran. Luas daerah tersebut merupakan selisih antara luas segitiga dan luas sektor lingkaran. Perhitungan ini melibatkan penggunaan rumus luas segitiga dan luas sektor lingkaran, yang bergantung pada panjang garis singgung dan sudut pusat yang bersesuaian dengan busur lingkaran.
Contoh Soal dan Latihan
Berikut disajikan beberapa contoh soal dan latihan untuk memperdalam pemahaman mengenai garis singgung lingkaran. Setiap contoh soal dilengkapi dengan langkah-langkah penyelesaian yang detail, sehingga memudahkan pembaca untuk memahami konsepnya. Latihan soal disusun dengan berbagai tingkat kesulitan, mulai dari yang mudah hingga yang lebih kompleks.
Contoh Soal 1
Tentukan persamaan garis singgung lingkaran x 2 + y 2 = 25 yang melalui titik (7, 0).
Penyelesaian:
- Cari titik singgung. Kita ketahui bahwa garis singgung tegak lurus dengan jari-jari pada titik singgung.
- Jari-jari lingkaran adalah 5. Garis yang menghubungkan titik (7, 0) dengan pusat lingkaran (0, 0) memiliki gradien 0/7 = 0.
- Gradien garis singgung tegak lurus dengan jari-jari, sehingga gradien garis singgung adalah tak hingga. Ini berarti persamaan garis singgung adalah x = konstanta.
- Substitusikan koordinat titik (7, 0) ke dalam persamaan x = konstanta, sehingga x = 7.
Contoh Soal 2
Sebuah lingkaran dengan pusat (2, -3) dan jari-jari 4. Tentukan persamaan garis singgung yang tegak lurus terhadap garis y = 2x + 5.
Penyelesaian:
- Gradien garis y = 2x + 5 adalah 2.
- Garis singgung tegak lurus dengan garis y = 2x + 5, maka gradien garis singgung adalah -1/2.
- Persamaan garis singgung dalam bentuk titik-gradien adalah y – (-3) = -1/2 (x – 2).
- Sederhanakan persamaan tersebut untuk mendapatkan persamaan garis singgung dalam bentuk umum.
Latihan Soal
Berikut beberapa latihan soal dengan tingkat kesulitan yang berbeda:
- Mudah: Tentukan persamaan garis singgung lingkaran x 2 + y 2 = 16 yang melalui titik (4, 0).
- Sedang: Tentukan persamaan garis singgung lingkaran (x-3) 2 + (y+2) 2 = 9 yang tegak lurus terhadap garis y = -x + 7.
- Sulit: Tentukan persamaan garis singgung persekutuan dari dua lingkaran dengan persamaan x 2 + y 2 = 100 dan (x-5) 2 + y 2 = 25.
Ringkasan Rumus dan Konsep Kunci
| Rumus/Konsep | Penjelasan Singkat |
|---|---|
| Persamaan garis singgung lingkaran x2 + y2 = r2 melalui titik (x1, y1) | x1x + y1y = r2 |
| Persamaan garis singgung lingkaran (x-a)2 + (y-b)2 = r2 dengan gradien m | y-b = m(x-a) ± r√(1+m2) |
| Garis singgung tegak lurus jari-jari | Konsep dasar dalam menentukan persamaan garis singgung. |
Ulasan Penutup
Dalam mempelajari garis singgung lingkaran, kita telah melihat berbagai aspek penting dalam geometri. Mempelajari teorema dan rumus-rumus yang terkait akan memperkaya pemahaman kita tentang hubungan antara garis dan lingkaran. Semoga materi ini bermanfaat dan dapat diaplikasikan dalam menyelesaikan berbagai soal geometri.